SPECTROSCOPIE - Spectroscopie des radiofréquences

SPECTROSCOPIE - Spectroscopie des radiofréquences

La spectroscopie des radiofréquences, ou spectroscopie hertzienne, désigne l’ensemble des études effectuées sur les phénomènes d’interaction résonante entre les atomes ou les molécules et les ondes hertziennes, c’est-à-dire les ondes électromagnétiques de fréquences relativement basses utilisées dans les transmissions radioélectriques. Ce phénomène d’interaction résonnante se produit lorsque la fréquence 益 de l’onde hertzienne est liée à la différence d’énergie entre deux états de l’atome par la classique relation de Bohr :

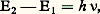où h est la constante de Planck (cf. mécanique QUANTIQUE). Il se traduit essentiellement par l’échange d’un photon d’énergie h 益 entre l’atome et l’onde hertzienne. La spectroscopie hertzienne constitue en fait une extension vers les basses fréquences 益 ou les grandes longueurs d’onde = c / 益 de la spectroscopie atomique ou moléculaire dont le développement initial s’était limité au domaine de l’optique.

Parmi l’ensemble des études de spectroscopie hertzienne, il faut mentionner la classe particulière des expériences de résonance magnétique où l’on étudie les transitions entre sous-niveaux magnétiques ou sous-niveaux Zeeman. La différence d’énergie E² 漣 E¹ est due à l’interaction entre le moment magnétique de l’atome (ou de la molécule) et le champ magnétique qui lui est appliqué; elle dépend du champ, et lui est proportionnelle tant qu’il reste assez faible.

On distingue parmi ces expériences de résonance magnétique deux grandes classes: si le moment magnétique du système atomique étudié est d’origine électronique (c’est le cas des corps paramagnétiques), on parle de résonance paramagnétique électronique (R.P.E.). Si les moments magnétiques des électrons ont, au contraire, une résultante globale nulle, on peut observer les effets des moments magnétiques des noyaux, bien qu’ils soient environ mille fois plus faibles que ceux des électrons; on parle de résonance magnétique nucléaire (R.M.N.). Pour le même champ appliqué, les fréquences de R.M.N. sont environ mille fois plus petites que les fréquences de R.P.E. La nullité du magnétisme électronique est le cas le plus général dans les molécules; cela explique l’usage intensif des expériences de R.M.N. par les chimistes, qui mesurent ainsi le champ microscopique créé par une molécule ou un groupement moléculaire au voisinage d’un noyau, avec toutes les applications qui en découlent.

Il existe un grand nombre d’autres phénomènes qui donnent lieu à des différences d’énergie assez faibles et qui sont étudiés en spectroscopie hertzienne: l’interaction «hyperfine» entre le moment électronique et le moment nucléaire du même atome ou du même ion, l’interaction d’un ion avec le champ électrique intense produit par les ions qui l’environnent dans un réseau cristallin (champ cristallin), la quantification des mouvements de rotation des molécules qui fait intervenir leurs moments d’inertie (cf. SPECTROSCOPIE – Spectroscopie moléculaire) et qui permet ainsi d’obtenir des renseignements sur les distances internucléaires, la forme des molécules, le rôle des isotopes, etc.

Dans toutes les études que l’on vient d’évoquer, les atomes ou les molécules se trouvent perturbés par les processus de relaxation, c’est-à-dire par les interactions microscopiques aléatoires avec les atomes ou ions voisins, soit dans le réseau cristallin, soit au cours des collisions en phases gazeuses. Les expériences de spectroscopie hertzienne permettent de mesurer la rapidité des processus de relaxation et d’obtenir ainsi des informations sur les interactions microscopiques aléatoires.

Les expériences de spectroscopie hertzienne ont fourni et fournissent encore des renseignements de grand intérêt sur la théorie de l’électrodynamique quantique , qui décrit les processus d’interaction entre les atomes et les ondes électromagnétiques. Elles ont aussi conduit à deux applications pratiques très spectaculaires: les magnétomètres de haute précision, fonctionnant même pour des champs magnétiques très faibles (la sensibilité peut être inférieure à 10^-9 G), et les étalons de fréquence, ou horloges atomiques, à partir desquels est maintenant définie l’unité de temps ^{[cf. HORLOGES ATOMIQUES]}.

1. Caractéristiques essentielles des transitions

Il n’existe aucune frontière théorique précise entre la spectroscopie hertzienne et la spectroscopie optique, pas plus qu’entre les ondes hertziennes et les ondes lumineuses. Mais le domaine intermédiaire, correspondant aux ondes millimétriques ou submillimétriques, a été encore peu exploré, et, de fait, la spectroscopie hertzienne s’est essentiellement développée dans le domaine des longueurs d’onde centimétriques ou métriques, utilisées pour le radar ou la télévision, ou bien dans le domaine des très grandes longueurs d’onde, utilisées pour la radiodiffusion. Les longueurs d’onde hertziennes sont ainsi supérieures au centimètre, alors que les longueurs d’onde optiques sont inférieures au micromètre; les premières sont donc au moins 10 000 fois plus longues que les secondes. Cet écart énorme d’ordre de grandeur donne à l’interaction onde-atome, dans le domaine des transitions hertziennes, des caractères sensiblement différents de ceux auxquels on était habitué pour les transitions optiques.

Absence d’émission spontanée

L’échange d’énergie entre le système atomique et l’onde de fréquence:

se produit selon trois processus distincts (cf. ATOME, MASER):

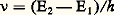– absorption de photons par les atomes qui se trouvent dans l’état d’énergie inférieur E¹: la probabilité par unité de temps pour que ce processus se produise est proportionnelle à la densité d’énergie 福 size=1^益 de l’onde de fréquence 益; on l’écrit B¹² 福 size=1^益;

– émission induite de photons par les atomes qui sont dans l’état d’énergie supérieur E²: les photons ainsi émis viennent renforcer l’onde incidente; ce processus est symétrique du précédent; sa probabilité est également proportionnelle à la densité d’énergie 福 size=1^益 et s’écrit B²¹ 福 size=1^益;

– émission spontanée de photons par les atomes dans l’état E²: les photons ainsi émis se répartissent au hasard dans toutes les directions de l’espace. Ce processus se produit avec une probabilité constante A²¹, même en l’absence d’une onde incidente.

C’est ce troisième processus qui est à l’origine de la lumière observée en spectroscopie optique lorsqu’on a porté les atomes dans les états d’énergie supérieurs en les excitant par une décharge électrique. Mais la théorie du rayonnement, mise sur pied par Einstein dès 1917 et perfectionnée après l’établissement de la mécanique quantique, montre que cette probabilité A²¹ est inversement proportionnelle au cube de la longueur d’onde:

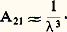Lorsque la différence d’énergie E² 漣 E¹ devient assez petite pour correspondre aux ondes hertziennes, la probabilité d’émission spontanée devient au moins 10¹² fois plus petite. Une probabilité aussi faible signifie que le processus n’est pratiquement plus observable. Seuls restent observables les deux autres processus, absorption et émission induite, dépendant de la densité d’énergie 福 size=1^益 de l’onde incidente. La transition entre les états d’énergie E² et E¹ ne se produit plus de manière spontanée et ne peut être observée que par interaction avec une onde incidente.

À la différence de la spectroscopie optique, une expérience de spectroscopie hertzienne exige l’emploi d’un appareil générateur d’ondes qui fonctionne indépendamment des atomes ou des molécules étudiés (exception faite des masers où l’on peut observer l’onde engendrée par émission induite; cf. MASER).

Suppression de l’effet Doppler-Fizeau

L’exactitude avec laquelle on peut mesurer une différence d’énergie E² 漣 E¹ dépend de la précision avec laquelle on détermine la fréquence correspondant à la relation de Bohr. De nombreuses causes peuvent intervenir pour limiter cette précision; mais la cause essentielle rencontrée en spectroscopie optique est l’effet Doppler-Fizeau lié aux mouvements des atomes.

On sait en quoi consiste cet effet: lorsqu’un émetteur et un récepteur d’ondes sont en mouvement l’un par rapport à l’autre avec une vitesse relative v, il en résulte un écart 嗀益 entre la fréquence 益 de l’onde émise et la fréquence 益 + 嗀益 mesurée par le récepteur. L’écart relatif de fréquence est égal au rapport entre la vitesse v du mouvement et la vitesse de propagation c des ondes électromagnétiques; on a 嗀益/ 益 = v/c . La relation est algébrique; en toute rigueur v est la composante du vecteur vitesse parallèle à la direction de propagation des ondes.

Dans leurs mouvements continuels d’agitation thermique, les atomes différents qui constituent la vapeur étudiée possèdent des composantes de vitesse v différentes réparties de façon aléatoire. La fréquence 益 + 嗀益 mesurée par l’observateur s’étale donc sur un certain intervalle de fréquence de largeur 益^D. On peut diminuer un peu 益^D en refroidissant la vapeur pour ralentir les mouvements d’agitation thermique; mais, de toute façon, le rapport 益^D/ 益 reste de l’ordre de grandeur de 10^-5 à 10^-6, et c’est lui qui limite la précision des mesures spectroscopiques dans le domaine de l’optique.

On remarque d’abord que l’effet Doppler a pour conséquence une erreur relative donnée 益/ 益. L’erreur absolue correspondante 益 varie donc proportionnellement à la fréquence 益, et sa valeur devient très faible lorsqu’on travaille avec les basses fréquences des ondes hertziennes: dans beaucoup de cas, l’erreur due à l’effet Doppler devient inférieure aux autres causes d’erreur.

On peut même obtenir une véritable suppression de l’effet Doppler. En effet, si les atomes sont enfermés dans un récipient de dimension l assez petite, ils heurtent fréquemment sa paroi, et leurs vitesses v changent à chacun de ces chocs; l’écart de fréquence 嗀益 correspondant au même atome change fréquemment de valeur et de signe. Si le processus d’interaction entre l’atome et l’onde n’est pas perturbé par les chocs, si enfin la dimension l est inférieure à la longueur d’onde, la théorie montre que les écarts 嗀益 successifs s’annulent, et on calcule un écart relatif moyen beaucoup plus petit que v/c . Les grandes longueurs d’onde des ondes hertziennes permettent de réaliser des récipients de dimension l inférieure à, et d’obtenir effectivement cette annulation de l’effet Doppler. On observe couramment des transitions hertziennes dont la largeur relative en fréquence 益/ 益 est inférieure à 10^-8, voire 10^-9.

2. Méthodes d’observation des transitions hertziennes

L’interaction entre l’atome et l’onde hertzienne se réduit à deux processus au lieu de trois; mais, pour obtenir le résultat global de cette interaction, il faut encore ajouter les contributions de ces deux processus qui ont des conséquences opposées. Pour ce faire, nous ajouterons l’hypothèse simplificatrice que les poids statistiques des deux niveaux d’énergie E¹ et E² sont égaux. Cela ne change rien aux lois essentielles des phénomènes mais simplifie un peu l’exposé parce que l’on démontre, dans ces conditions, que les deux coefficients B¹² et B²¹ sont égaux: B¹² = B²¹ = B.

Appelons n ¹ le nombre d’atomes qui se trouvent dans l’état d’énergie inférieur E¹ et sont seuls susceptibles de subir le processus d’absorption. Appelons n ² le nombre d’atomes qui se trouvent dans l’état d’énergie supérieur E² et sont seuls susceptibles de subir le processus d’émission induite. Les nombres n ¹ et n ² sont encore appelés les populations des niveaux d’énergie E¹ et E². On désigne par P le nombre de photons de l’onde incidente. L’évolution au cours du temps des populations n ¹ et n ² s’obtient en écrivant simplement les définitions des probabilités de transition par unité de temps.

Sous l’action du processus d’absorption seul, la population n ¹ diminue et sa variation algébrique ( 嗀n ¹)^abs pendant la durée 嗀t est donnée par:

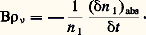Sous l’action du processus d’émission induite, agissant seul, la population n ² diminue, et sa variation algébrique ( 嗀n ²)^ind, pendant la durée 嗀t , est donnée par:

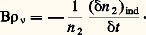Mais chaque fois qu’un atome, un ion ou une molécule quittent l’état 1, ils arrivent dans l’état 2 et réciproquement, c’est-à-dire que le processus d’absorption provoque une augmentation de la population n ² telle que:

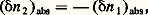et le processus d’émission induite provoque une augmentation de la population n ¹ telle que:

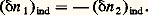On obtient la variation globale des populations en ajoutant algébriquement les contributions des deux processus:

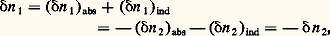et on en déduit finalement:

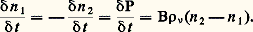Si l’on a n ¹ = n ², toutes les variations calculées sont nulles; les deux processus d’absorption et d’émission induite se compensent exactement en sorte qu’aucune modification macroscopique du système ne se produit. On observe une modification du système physique à condition seulement que les populations n ¹ et n ² des deux niveaux d’énergie soient inégales; cette modification sera d’autant plus importante que cette inégalité de populations sera plus grande. On distinguera dans ce qui suit les diverses méthodes d’observation utilisées en spectroscopie hertzienne suivant la manière dont on obtient cette inégalité de populations.

Inégalité des populations thermiques

Lorsque l’équilibre thermique se trouve réalisé dans un milieu, la répartition des atomes entre les divers états se trouve imposée, conformément à la loi thermodynamique de Boltzmann qui fixe les rapports de populations ^{[cf. POMPAGE OPTIQUE]}:

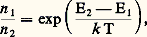où k est la constante de Boltzmann et T la température absolue. Le niveau inférieur E¹ est ainsi plus peuplé que le niveau supérieur E², et cette différence de populations est, dans beaucoup de cas, suffisante pour permettre la détection d’un affaiblissement de l’onde à la traversée de l’échantillon étudié: E² 礪 E¹ entraîne n ¹ 礪 n ², et l’absorption l’emporte sur l’émission induite.

En fait, la loi de Boltzmann impose le rapport des populations, c’est-à-dire leur écart relatif :

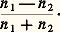L’énergie absorbée est proportionnelle au contraire à l’écart absolu n ¹ 漣 n ² des populations. Lorsqu’on étudie un échantillon de matière condensée, solide ou liquide, le nombre total d’atomes n’est pas tellement inférieur au nombre d’Avogadro, et l’énergie électromagnétique absorbée est assez importante pour fournir une méthode de détection très confortable. C’est la méthode couramment employée dans les études de R.P.E. (résonance paramagnétique électronique) et de R.M.N. (résonance magnétique nucléaire), suivant les techniques mises au point, à partir de 1945 par E. Zavoisky pour la R.P.E. et à partir de 1946 par Bloch, Purcell et Pound pour la R.M.N.

Cette méthode s’applique aussi à des gaz si leur pression est suffisamment forte. Mais elle n’est plus applicable dans le cas où le nombre d’atomes est trop faible parce qu’on étudie une vapeur sous très faible pression ou un jet atomique (ce sont précisément les conditions dans lesquelles les atomes ou molécules subissent les perturbations les plus faibles et permettent donc les mesures les plus précises); elle n’est pas applicable non plus lorsque la fréquence de transition est très basse (c’est le cas de la R.M.N. dans les champs magnétiques faibles).

Triage sur un jet atomique

On forme un jet atomique en laissant les atomes d’une vapeur pénétrer dans une grande enceinte parfaitement vidée d’air à travers un mince canal (cf. jets et faisceaux MOLÉCULAIRES). Seuls les atomes dont la vitesse est à peu près parallèle à l’axe du canal parviennent à le traverser (les autres viennent se coller sur la paroi du canal) et, ne rencontrant plus aucun obstacle, ils continuent dans la grande enceinte leur trajectoire rectiligne dans le prolongement du canal (la force de pesanteur est négligeable). Les atomes qui se trouvent dans des états différents peuvent être soumis à des forces distinctes, voire opposées, lorsqu’on leur fait traverser un champ électrique ou magnétique de configuration appropriée; on peut ainsi obtenir que les atomes dans l’état E¹ voient leur trajectoire déviée à droite pendant que les atomes dans l’état E² voient la leur déviée à gauche. Le jet atomique initial se trouve ainsi divisé en deux jets distincts dont chacun ne contient que des atomes appartenant à un seul état et se prête particulièrement bien à une expérience de spectroscopie hertzienne.

La détection des transitions peut exceptionnellement se faire sur l’onde: c’est le cas très particulier du maser de Townes ^{[cf. MASER]}. Mais le nombre d’atomes dans un jet est si faible que la détection sur l’onde est généralement impossible, malgré la proportion (100 p. 100) d’atomes dans un seul état. On détecte alors les atomes qui changent d’état au cours des transitions hertziennes. Le prototype de cette méthode est l’expérience réalisée en 1938 par Rabi pour étudier la R.M.N.; cette méthode a connu de très riches développements. À quelques variantes près, la même méthode peut être utilisée pour étudier les transitions de la R.M.N. dépendant du champ magnétique appliqué ou les transitions hyperfines, indépendantes du champ magnétique, utilisées dans les horloges atomiques ^{[cf. HORLOGES ATOMIQUES]}.

Techniques de pompage

Certaines techniques permettent de créer artificiellement une différence de populations n ¹ 漣 n ² supérieure à la normale en pompant les atomes d’un niveau à l’autre, comme on pompe l’eau d’un réservoir à un autre. Ces techniques très variées reposent sur une étude détaillée des interactions microscopiques qui perturbent les états atomiques: interactions entre le spin nucléaire et le spin électronique du même atome, interaction entre les spins d’atomes ou d’ions d’espèces différentes, processus de relaxation qui réalisent l’équilibre thermique par interaction avec le réseau cristallin. Dans tous les cas, le processus de pompage est obtenu en saturant une autre transition atomique avec une onde électromagnétique de forte puissance à une fréquence différente de celle que l’on étudie. Ce peut être une transition hertzienne sur des atomes différents de ceux que l’on étudie (polarisation dynamique d’Abragam), ou bien une transition hertzienne entre d’autres niveaux d’énergie de l’atome étudié (maser à trois niveaux de Basov, Prokhorov et Bloembergen), ou enfin transition optique sur le même atome (pompage optique de Kastler ^{[cf. POMPAGE OPTIQUE]}.

Les applications de ces techniques de pompage sont très nombreuses, et elles permettent en particulier de réaliser, dans de nombreux cas, l’inversion de population (n ² 礪 n ¹) nécessaire au fonctionnement des masers.

Peuplement sélectif d’états instables

Lorsqu’on étudie une transition entre deux états atomiques instables qui n’existent pas à l’équilibre thermique (états excités ou métastables), il faut utiliser un processus qui porte les atomes dans ces états. Si ce processus est bien contrôlé, il permet de peupler l’un des états plus que l’autre, réalisant ainsi l’inégalité de populations souhaitée. De nombreuses études de spectroscopie hertzienne ont été effectuées sur des états atomiques excités peuplés sélectivement soit par bombardement électronique (il faut que l’énergie cinétique du faisceau d’électrons ne soit pas trop élevée), soit par excitation optique (il faut utiliser de la lumière polarisée).

Encyclopédie Universelle. 2012.